Joe Maller: FXScript Reference: Building Joe's Radial Desaturate
How I used FXScript to build my Radial Desaturate filter for Final Cut Pro.Visit the New FXScript Reference and Joe's Filters sites. These pages will be phased out soon and may already be out of date.
This page describes the FXScript concepts behind Joe's Radial Desaturate. If you're looking for the page about how to use the filter, click here.
Overview
Joe's Radial Desaturate recreates an effect I've been creating in Photoshop with the channel mixer. A mix of the three color channels are combined to create a grayscale image specific to a given color. The effect is very similar to using a colored glass filter when shooting black and white film, different colors result in grayscale tonal ranges which might otherwise be missed.
After Building Joe's RGB Desaturate, I realized that each channel could be increased relative to one-another to create a grayscale image from any point around the hue wheel. When I started this, I had only the slightest understanding of Matrix Math and a hunch that the math would be simple. The hunch was right, but it took a long time to figure it all out.
How it works
The beginning of the script is standard, a definition, group and three inputs:
filter "Joe's Radial Desaturate";
group "Joe's Filters";
input desat, "Saturation", Slider, 100, 0, 100 label
"%"
The Saturation slider indicates a range from complete color replacement to complete desaturation.
input r, "Hue Angle", Angle, 0, -360, 360
input colorizer, "Original", Slider, 0, 0, 100 label "%"
The angle selector value is transformed into three values with the foloowing equasion
Because each color will return a value between 1 and 0, and will overlap one other color, depending on the color, the maximum combined value for each color is 2. A value of two would indicate a secondary color, Cyan, Magenta or Yellow. Values of 1 must be a primary color, Red Green or Blue.
Playing around with Joe's 3x3 Matrix Fun filter shows that for an image's luminance to be preserved the total values must not exceed one for any of the three colors.
The Color Wheel
While working out how the angle selector would work, I realised something that seems obvious to me now (and should have been obvious to begin with. Each of the three color primaries are each full intensity for 120° of the color wheel. Each then graduates off for another 60° on either side of that. I was initially mistaken in thinking the primaries faded immediately out from their pure state.
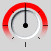 +
+  +
+ 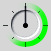 =
= 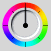
In looking at the color wheel dissected, it's very clear that each set of neighboring primary colors finish their gradiations at the full intensity point of whichever color is left over.
Adjusting the desaturation about halfway and then subtly shifting the hue wheel can produce interesting tint effects
Translating Angles
Now that I understood how the color wheel worked from a mathematical point of view, the script needed to convert a single angle value into three distinct color values. This was not as fast as I'd hoped.
Early in the script, the value of r (the hue angle input selector) is adjusted:
r = (r + 360 )mod 360
This is to compensate for the allowing the input to move 360° in both directions.
Incidentally, this is also when I learned about the concept of Modulo.
if r < 180;
rangle = (abs(r) - 60)/60;
else;
rangle = (abs(r - 360) - 60)/60;
end if
if rangle >= 1; rangle = 1; end if
if rangle <= 0; rangle = 0; end if
gangle = (abs(r- 120)-60)/60
if gangle >= 1; gangle = 1; end if
if gangle <= 0; gangle = 0; end if
bangle = (abs(r - 240)-60)/60
if bangle >= 1; bangle = 1; end if
if bangle <= 0; bangle = 0; end if
This was the second filter I wrote, and this code is somewhat embarrassing. There are several errors here but unfortunately this page was not completed until after I released the filters. Instead of explaining how that works, I'm going to take this opportunity to show how that should work.
The sets of if statements for rangle, gangle and bangle are redundant.No they aren't. They are trapping values between zero and one, otherwise they would be all on all the time. Moron.
If the value returned by rangle is greater than or equal to one (rangle >= 1), rangle is reassigned to one. If rangle is less than or equal to zero (rangle <= 0), then rangle is reassigned to zero. The goal of this code is to trap the values between zero and one by disallowing any values beyond this range. the variables gangle and bangle work the same way.
othewise these fixes would have been corrected.
This filter was written before I learned about Trinary Operators, which could have reduced the above code down to 6 lines.
note: In the released version of the filters, there was a mysterious 120 after the r<180. This must have been a leftover from my trying to figure this out, but the real mystery is why this didn't cause everything to blow up? If you'd like to fix this in the paid version of Joe's Filters, just delete the 120, it has no effect.
I spent a long time fussing around with the angle input. I had trouble coming up with a simple way of getting the values into the channels. Originally I suspected there might be a very elegant way of moving using the angle value with no if-else statements, but after spending most of a Saturday morning trying, I eventually gave in to one if-else statement with a set of additional statements for capping the high and low values. It's probably not the most elegant solution, but it works.
The Solution
The solution I came up with is based on this formula:
In trying to work out how to get the colors to move across the matrix, I knew I had the following values to work with:
Current = current value of each color
Desaturate = Desaturation amount from slider
Target = Target value for each primary (0.33)
Those three values were then combined into the following formula:
Current - Desaturate * (Current -Target)
How it works
I used two inputs, a popup named RGBTarget and labeled "Source"; and a slider named desat and labeled "Saturation". The slider has values go from 0 to 100.
For the matrix, I decided to enter values as variables since it was easier for me to think about, so I declared the following floating point Variables:
float rr, rg, rb, gr, gg, gb, br, bg, bb, offset0[3], mat[3][3],
greypoint[3][3], temp[3][3], rdif, gdif, bdif, i;
See my 3x3 Matrix Fun filter for a more detailed explanation of how the 3x3 matrix works for RGB.
r, g, and b variables refer to thwhich apply to the matix as follows:
neo [3] [3] |
||||||
| rr | rg | rb | [0][0] |
[0][1] |
[0][2] |
|
| gr | gg | gb | [1][0] |
[1][1] |
[1][2] |
|
| br | bg | bb | [2][0] |
[2][1] |
[2][2] |
|
The filter will take move data from one channel into another, depending on the selected method of desaturation.
The clunkiness of the Blue channel is the result of compression in the YUV encoding. Read this page for more information:
I built this filter with each of the 9 entries of the 3x3 matrix as searate variables. Partly I did this because it's easier for me to work with, partly because I don't understand 3x3 matrix math much at all. It seems to make sense, but it hasn't been in my head long enough to make use of it yet.
The FXScript Reference
FXScripting Joe's Filters
Joe's Filters for Final Cut Pro
Building Joe's Minimum Maximum
Joe's FXScript Explorers
Joe's Debug and Explore Filters
Joe's 3x3 Convolve Matrix Tester
Joe's 3x3 Matrix Values Tester
Other FCP Stuff
Film & Video
Recording the sound of
one eye blinking
Photography
Projects
Final Cut Pro
Design
WRITING
Site Notes Archive (weblog)
Web Resources
About Joe Maller
Past Home Pages Etc.
Search joemaller.com
Contact Me
